Popular Science Monthly Volume 19 August 1881 (1881) Theodore Wehle
ORIGIN AND HISTORY OF LIFE INSURANCE. #
LIFE insurance is based upon the theory that there is a law of mortality governing life; that is to say, that at all ages from birth to the utmost limits of life a certain proportion of individuals will die during fixed periods. Not that the precise duration of an individual life can be predicted, but that the ratio of deaths out of large gates will remain the same under similar conditions. This conception, so self-evident to-day, was slow to dawn upon the human mind. Ancient pagan belief, various forms of superstition, as well as theology, all assumed life to be under the special control of a mysterious and arbitrary power. The conviction that it is subject to laws, as unalterable as those that govern the physical universe, has only gained ground within a comparatively recent period. Nor could such a view assert itself until mathematics and statistics had reached a certain degree of perfection; for, previous to that, the law of averages and probabilities, as applicable to social problems, could not be understood. Even after science had taken the initiative, and formulated the law upon such data as were accessible, a long period elapsed before steps were taken to apply its principles to practical ends. The conditions of society were as yet too unsettled, property and life too insecure, to permit such experiments. Not until after the middle of the eighteenth century did the desire to provide for widows, orphans, and other dependents, become so general as to lead to the establishment of a life-insurance society in London.
Since then the system has been steadily perfected, and has grown to considerable dimensions all over the civilized world. At present more than 600,000 lives are insured in the United States alone; and the usefulness of the institution is only beginning to be properly appreciated. In view of this fact, and of the general interest that cooperative enterprises are attracting just now, it may be well to point out that life insurance must be reckoned among the grandest and most successful efforts ever attempted in that direction. It has, moreover, a century’s experience to attest the strictly scientific principles upon which it rests. Such an institution well deserves to be better and more generally understood; but, however large the number directly interested, it is strange how few have correct notions about it. This is probably attributable to the character of the literature on the subject, which, addressed to specialists, employs many technical terms, or, intended for soliciting agents, contains mere platitudes. Thus the impression prevails that it is either too dry or veiled in too much mystery to deserve the attention of even the educated classes.
It will be the aim of these articles, while giving an outline of the origin and history of mortality-tables, the results attained, and an explanation of the practical working of the whole system, to present it in so plain and popular a manner as to be readily understood by every intelligent reader.
I. Origin and History.—Among the nations of antiquity, the Romans were the first to make an effort to arrive at a law of mortality. To this they were led indirectly by their highly developed system of jurisprudence. It became necessary at times to fix the value of life-estates, i. e., property owned during lifetime only, without the right of alienation or bequest, and to do so the probability of life had to be estimated. It appears that the method in common use was about equivalent to assuming that all persons who attain the age of thirty would certainly live to the age of sixty, and then certainly die. This purely arbitrary assumption was probably accepted by jurists as the simple solution of a difficult problem.
A great improvement was introduced by the Prætorian Prefect Ulpianus, one of the most eminent of Roman jurists. He published a table of mortality, in which a distinction was made between the different ages, and the probable number of years of life for each given. The rate of mortality assumed for the middle ages approximates to that probably prevalent previous to the seventeenth century. Whether this table was based upon actual observation or was purely speculative is not settled; but, if its estimates were correct, the chances of life above sixty years were very poor indeed among the Romans. However, these early efforts do not seem to have exercised any influence toward a proper investigation of the subject, and, having been forgotten, they only possess a passing interest for us.
The real germs from which life insurance ultimately developed were life-annuities and tontine annuities. These latter derived their name from a Neapolitan adventurer, Tonti, who came to Paris in 1653, in the reign of Louis XIV. He formed associations based upon the agreement that members should pay a certain sum of money into a fund, which was to be managed by him or other founders. The interest on this capital was annually divided among the surviving members, and, as their number grew smaller, their income became larger from time to time, until eventually the last survivor enjoyed the whole annual proceeds, which often were considerable. An instance is given of a widow who died in France in 1726, at the age of ninety-six, as the last survivor of a tontine society, having an income of 79,000 francs; her husband had been a surgeon, and had paid 300 francs for her membership in the association.
Such schemes were naturally attractive, and spread rapidly over Europe. Various modifications were introduced, adapting them to changing circumstances. Even governments had recourse to them as a means of raising money, when credit was low. The English Government made a tontine loan in 1693, comprising 1,002 members, the last of whom died in 1783. The other, known as the Great English Tontine, was started in 1789 for £1,000,000, embracing about 3,500 lives.
Voluntary associations for specific purposes were also quite frequent. One of a later date, originating in this city, may be mentioned by way of illustration. The Tontine Association of New York, established in 1794 by prominent merchants, upon 203 shares, applied its fund of about $40,000 to the erection of a coffee-house at the corner of Wall and Water Streets. There was an agreement that, when the nominees (mostly young children of the originators) should be reduced to seven, the association should come to an end. Accordingly, in 1870, the requisite number being reached, steps were taken to have the property (which was then valued at $200,000) divided.
The advantages the tontines seemed to offer made them very enticing. The larger the number of deaths a prospectus would promise, the greater the expected gain to the survivors. No reliable calculation or precise prediction of the mortality was necessary, since they were to be guided by the actual experience only. But the very ease with which they could be formed tended to make them deteriorate into little better than mere lottery schemes, used by designing men to plunder the credulous.1
At present the tontine principle does not enlist our sympathy, being too selfish for our times, but it probably answered a good purpose in its day. Life and property were insecure, the investment of small sums difficult, the usury laws stringent: how natural for men to look to immediate enjoyment, when provision for the future was surrounded by so many uncertainties!
Nor is it likely that Tonti was the real originator of the idea. There is reason to assume that similar customs had taken root in Italian cities long before his time. Probably the same conditions and needs of society also led to the practice of purchasing life-annuities. It seems to have been a favorite mode of raising money, among the flourishing towns of the Netherlands, since the early part of the sixteenth century. On the payment of a certain sum to the party granting the life-annuity, a fixed annual income could be secured during lifetime.
Two other methods of making loans were also known to these old communities, namely, terminable and perpetual annuities.
Terminable annuities are such as are redeemable after a fixed number of years, and bear interest until maturity. That is the usual mode of investing funds at present.
Perpetual annuities are those that bear interest for ever, while the principal never becomes payable. Many European governments have funded their debts upon that principle, the most noted being the French rentes and the English consols.
The people of the Netherlands, that so early displayed commercial and political activity, continued to grow in importance until, by the middle of the seventeenth century, they ranked among the foremost nations of Europe. The freedom they enjoyed fostered material prosperity and encouraged the arts and sciences. Their statesmen and officials were often men of the highest attainments.
One of the greatest among these was Jan de Witt, Grand Pensionary of Holland and West Friesland, a disciple of Descartes, and author of a mathematical work of note.
About contemporary with him, the eminent French thinker, Pascal, had laid down the first principles of the doctrine of chances. The celebrated Christian Huygens enlarged upon these inquiries in a treatise written in Dutch. When, in 1671, the States-General applied to De Witt to elaborate the best plan for raising a loan, he was the first to apply the principles of the science to a practical subject. In a memorable report he states that, for reasons given, it is better to negotiate funds by life-annuities, which by their nature are terminable, than to resort to either perpetual or terminable annuities. He shows that it had long been the practice in Holland to grant life-annuities at double the rate of interest current. That is to say, if four per cent, was customary, a loan of one hundred florins would bring four florins per annum, while one hundred florins applied to the purchase of a life-annuity would yield an income of eight florins. He goes on to prove that the practice of making no distinction between the ages, the selling a life-annuity on the same terms to the young and the old, was based on a fallacy. He then applies the doctrine of chances to data, most likely deduced from former annuity experiences, and proceeds to construct a mortality-table. This table, though erroneous in many respects, is still the first application of mathematical principles to questions of this kind, and, as such, deserves the highest consideration.
The report was never acted upon, and was lost before De Witt’s contemporaries had become acquainted with it.
Toward the end of the seventeenth century, the subject of calculating a table of mortality began to create interest in scientific circles in England; but the difficulty was, to obtain reliable statistics. A few registers had been kept since 1538, and by 1600 they had been introduced into probably one half the parishes of England. Unfortunately, only births or baptisms had been entered. During the plague, the government was induced to publish mortality bills, showing the number of deaths; but here, also, the ages were not stated. The Royal Society, finding no data at home, turned to the Continent of Europe.
The city of Breslau, in Silesia, had kept an exact register of births and deaths for some time, and reliable copies for the five years from 1687 to 1691 were obtained. These were intrusted to the Astronomer Royal, the celebrated Dr. Halley, renowned for having calculated the orbit of a comet, which has been named after him. He published a treatise, which appeared in the “Philosophical Transactions” in 1693, giving the following mortality-table, the first that had ever been constructed on exact scientific principles:
BRESLAU TABLE.
| Age. | Living. | Age. | Living. | Age. | Living. | Age. | Living. | Age. | Living. |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1000 | 19 | 604 | 37 | 472 | 55 | 292 | 73 | 109 |
| 2 | 855 | 20 | 598 | 38 | 463 | 56 | 282 | 74 | 98 |
| 3 | 789 | 21 | 692 | 39 | 454 | 57 | 272 | 75 | 88 |
| 4 | 760 | 22 | 586 | 40 | 445 | 58 | 262 | 76 | 78 |
| 5 | 732 | 23 | 579 | 41 | 436 | 59 | 252 | 77 | 68 |
| 6 | 710 | 24 | 573 | 42 | 427 | 60 | 242 | 78 | 58 |
| 7 | 692 | 25 | 567 | 43 | 417 | 61 | 232 | 79 | 49 |
| 8 | 680 | 26 | 560 | 44 | 407 | 62 | 222 | 80 | 41 |
| 9 | 670 | 27 | 553 | 45 | 397 | 63 | 212 | 81 | 34 |
| 10 | 661 | 28 | 546 | 46 | 387 | 64 | 202 | 82 | 28 |
| 11 | 653 | 29 | 539 | 47 | 377 | 65 | 192 | 83 | 23 |
| 12 | 646 | 30 | 531 | 48 | 367 | 66 | 182 | 84 | 20 |
| 13 | 640 | 31 | 523 | 49 | 357 | 67 | 172 | 85 | 15 |
| 14 | 634 | 32 | 515 | 50 | 346 | 68 | 162 | 86 | 11 |
| 15 | 628 | 33 | 607 | 51 | 335 | 69 | 152 | 87 | 8 |
| 16 | 622 | 34 | 499 | 52 | 324 | 70 | 142 | 88 | 5 |
| 17 | 616 | 35 | 490 | 53 | 313 | 71 | 131 | 89 | 3 |
| 18 | 610 | 36 | 481 | 54 | 302 | 72 | 120 | 90 | 1 |
Considering the disadvantages under which he labored, it was a wonderful production. He had no record of the whole population, and only 6,193 births and 5,869 deaths of all ages from which to draw his deductions.
The form of the table has been substantially retained to the present day. It begins with 1,000 children, in the first year of life, of whom 145 die in the course of the year. At the beginning of the second year there are 855 living, of whom 66 die in the course of that year; and so the table continues until, at the age of 90, the last one of the original number will die. The probability of dying in any one year of life is readily ascertained. For instance, in the first year of life, 145 die out of 1,000. Therefore, the probability of dying is \(\frac{145}{1000}\) =·145. In the second year 66 die out of 855, which makes the probability \(\frac{66}{885}\) =·077. That is to say, according to Halley’s table, 14\(\frac{1}{2}\) per cent. of all newly-born children will die in the first year of life, and about 7\(\frac{3}{4}\) per cent. in the second year. Another interesting deduction pointed out by him is what a modern actuary has called the equation of life. It will be observed that, out of 1,000 at age 1, 499 will survive at 34, which indicates that the chances of dying or living to age 34 are about equal for a child at birth. It may be applied to any other age. At 19 the table shows 604 living, while at 54 there are 302; therefore, a youth at 19 has, to age 54, an equal chance of living or dying.
Whether Halley’s table is a correct exposition of the mortality of the time it is difficult to say, since his data may have been insufficient; but the reasoning on which it was based and the conclusions drawn were strictly scientific.
But, while Halley’s treatise must have been highly appreciated by mathematicians, the public at large seemed to have remained ignorant of its value. Life-annuities continued to be sold on mere conjecture. Even the English Government made no distinction between different ages in the early part of the eighteenth century. A child at ten years could obtain a life annuity of £100 for £714, while it was probably worth over £1,300 at that time.
It is not within the province of this article to trace in detail the progress made in the science of life contingencies. Nearly every mathematician of note contributed to the perfection of the theory, while it was left almost exclusively to England to apply it in practice.
Passing over minor writers, Thomas Simpson, a self-taught mathematician, a mind of great originality, next deserves notice. In 1742 he enlarged upon the theory of Halley, De Moivre, and others, and, deeming the Breslau table not applicable to English conditions, he compiled and computed a mortality-table from the London mortality bills from 1728 to 1737. For a number of years he published pamphlets and delivered lectures on the subject, attracting the attention of the public at large.
Shortly thereafter James Dodson, also a very able mathematician, employed Simpson’s tables, and made many valuable additions and suggestions thereto. He contributed a number of able papers to the “Philosophical Transactions,” and was the first to point out, in 1755, how mortality-tables might be applied to the calculation of life-insurance premiums.
Up to this time, it will be noticed, life insurance in the modern sense was unknown. Both tontines and annuities had the very opposite object in view, sacrificing the whole capital for an increased income during lifetime. The reasons that made tontines popular have been briefly touched upon. Similar causes applied to life-annuities; besides, they provided a convenient way of evading the usury laws, and were often resorted to for that purpose. It was impossible to discriminate what part of the high rate of interest paid was for the use of money, and what percentage was due to the chance of death.
But, while life insurance as a system is of recent date, the practice of effecting temporary insurance on lives had its origin with the rise of marine insurance, probably as early as the fourteenth century. It was no more, however, than a mere bet, not based upon any experience or estimate, and led to many immoral devices. On that ground it was declared unlawful, and prohibited in the Netherlands, Spain, and Italy, together with other wager contracts, as far back as the fourteenth and fifteenth centuries. In England, however, there was no restriction, and, in the eighteenth century, betting on the lives of prominent men was carried on regularly at Lloyd’s and other coffee-houses in London.
The spirit of gambling, that set in with the South-Sea bubble in 1720, continued to ebb and flow until the statute against wager contracts was enacted in 1773. It gave rise to a large number of wild insurance schemes, most of which were ridiculous, while many were intentional frauds. The failures that necessarily followed created distrust and retarded the efforts that were just beginning to be made to introduce legitimate life insurance.
But a new era had begun in the history of the English people. The cessation of internal strife, the settlement of fundamental, constitutional questions, the increase of material prosperity, the greater power and intelligence of the people, and the growth of large towns, particularly London, had completely changed the conditions of society as compared with previous centuries. Selfishness and brutality gradually yielded to more forethought and refined feeling; family ties grew warmer and more generous. Comforts were greater, life and property more secure, and everything tended to a more vivid desire in thoughtful men to provide for their families in the contingency of their own death. The feeling was most pronounced among the clergy and other professional classes, and associations began to form to accomplish that purpose. The conditions on which they were based were somewhat similar to those even now in vogue, with benevolent institutions having the same object in view. On the death of a member, his heirs would receive a certain contribution from the surviving members.
Such arrangements, when a mere subordinate feature of benevolent societies, may work well for a time, but they can not serve as substitutes for life-insurance companies. These can only be founded on scientific principles, and all other devices must be futile and short-lived, as a century’s experience has amply shown. The difficulties to be encountered were clearly foreseen and explained by the mathematicians of the day, and their labors did not prove in vain. In 1761 a number of gentlemen petitioned Parliament for a charter for a life-insurance association. They met with opposition, on the ground that the undertaking was purely speculative, devoid of any merit, and sure to fail. The charter not being granted, they organized in 1765, as a mutual insurance company, under the title of “The Equitable Society.”
They were the first to issue policies for life, for a fixed amount, and at premiums not merely conjectural. Still, for a number of years their progress was very slow. But the public mind was agitated on the subject, and many men of superior ability were absorbed by it. Most prominent among these was Dr. Price, an unsuccessful Unitarian preacher, who had contributed many excellent papers to the “Philosophical Transactions,” and published treatises on annuity values. He was consulted by one of the many insurance societies then forming, all of which he found started on a basis sure to lead to ruin. As he expressed it, “All London seems to be entering societies of this sort,” and he determined to examine the subject thoroughly. What appeared an easy task proved the arduous labor of many years. The London mortality bills could not serve as a proper basis for insurance calculations. The large and fluctuating population of a city like London, with its extremes of social conditions, could not be deemed a fair exponent of the value of healthy lives of the whole country. Dr. Price set to work to collect data from which trustworthy tables might be computed. He constructed quite a number of them, among which, one based on thirty years’ mortality of Norwich, and another on ten years’ observation at Chester, attracted considerable notice. He also applied such French, Dutch, and Swedish statistics as were available. But most important of all, and the one on which his fame chiefly rests, was the Northampton table, taken from thirty years’ mortality observations of the town of Northampton. At the time of its publication, Dr. Price’s numerous works had become widely known and his reputation was well established. In 1780 the Equitable Society, which had commenced with Dodson’s London tables, concluded to adopt the Northampton table, and Dr. Price became the Society’s consulting actuary. The directors generally followed his suggestions, and within a year he made 20,000 computations for them. The Society, now basing the reserves on the Northampton table, which showed a lower rate of mortality than Dodson’s, found the surplus to accumulate rapidly, and large and frequent dividend additions were made to the old policies. With the reduction of the premiums the business increased steadily, and numbers of new companies were started in competition, whose fate we need not follow. Life insurance had become a practical system, established on a scientific basis.
The directors of the Equitable Society were intelligent and enterprising but very careful men. They had selected the Northampton table, from the different new tables presented, because among these it showed the highest rate of mortality. It proved to be based on a peculiar error of reasoning. An enumeration of the whole population could not be obtained, and the parish registers only gave a record of the christenings and deaths. But the town contained great numbers of Baptists, who repudiate infant baptism; and Dr. Price overlooked the fact that births and christenings were not identical, and assumed a much higher proportion of deaths to births than had actually occurred. The Northampton table came into general use, however, and the English Government, that had adopted it as a basis for annuity values, lost about £2,000,000 before its inaccuracy was discovered.
The next step of importance was the publication of a new mortality table, known as the Carlisle table, by an eminent actuary, Mr. Joshua Milne, in 1816. It was deduced from data obtained from the town of Carlisle, a very healthy and prosperous place, growing both by immigration and natural increase. During the eight years from 1779 to 1787 the population had risen from 7,077 to 8,677 inhabitants, being just 1,000, and the deaths recorded were 1,840. While the number under observation was very small, the advantage of having enumerations of the whole population was considerable. For the first time it was possible, not only to compare births and deaths, but also to determine their proportion to the living. With the exception of the very young and old ages, where the numbers had been too few to make it reliable, the excellence of the Carlisle table was so pronounced that it quickly superseded the Northampton table, and remained in use until within a very recent period. With its adoption, premiums were again lowered, and the business increased largely. It outgrew the experimental stage, and, until then confined to England, began to extend to the Continent of Europe.
MODERN BASIS OF LIFE INSURANCE. #
WITH the year 1839 a new phase is reached in the first effort to tabulate the actual experience of insurance companies. Heretofore the average life of towns had furnished the data for mortality tables; now a table was to be deduced from observations of insured lives. Seventeen leading offices appointed a committee, to whom copies of their records were to be intrusted, which, owing to jealousies, were not as perfect as desirable. In 1843, after years of labor, a table was published, now known as “Actuaries’ Experience Table No. 1.” It was based on 18,282 policies, of which 7,372 had been discontinued, 4,786 had terminated by death, and 6,124 were still in force. The average duration of the policies under observation was eight and a half years,
In 1869 a table taking a far wider range was compiled, known as “Actuaries’ Experience Table No. 2.” It comprised the experience of twenty English and Scotch offices, all over twenty years old. It treats of 146,847 lives, which on an average had been under observation for ten years, and records 23,856 deaths. This table was not graduated until recently, and is only beginning to come into use.
About the same time Mr. Sheppard Homans published the “American Experience Table,” based principally on twenty-six years’ experience of the Mutual Life Insurance Company of New York. For the very young and old ages where the data were insufficient, he also made use of other American and English statistics. This table has been adopted as the official standard for New York and many other States.
The exact numbers and other details that served as a foundation for all these mortality tables have been given rather fully, at the risk of wearying the reader. The object has been to indicate the difficulties of obtaining them in a reliable and sufficient form, and on such a scale as to furnish trustworthy averages.
A little reflection will show that large numbers must be observed for a long term of years, to have deaths occur for every single year of life, and in the proper proportion for each age. Take as an illustration the Carlisle table based upon 1,840 deaths in eight years, which would average 230 deaths per year. According to the present mortality of England, about forty per cent. of the deaths of the whole population occur among children under five years old, forty per cent, between the ages of five and sixty-five, and twenty-per cent, in old age, between sixty-five and one hundred years. Apply these percentages to the 230 deaths at Carlisle, and they would give 92 persons dying under five years old, 92 between five and sixty-five years, and 46 between sixty-five and one hundred years of age. For the last thirty-five years of life only 46 deaths would be likely to take place, because, while the percentage of mortality is high, the number living at those ages is very small. But, when 46 deaths are distributed among thirty-five years of life, it is apparent that they are not likely to prove regularly divided among them. At some ages, and they may be the very highest, no deaths at all may occur. We know, however, that it is not in the course of nature that in any one year of life no human being should die, and properly ascribe it to the small number and the short space of time observed. Here the mathematician steps in and determines, from the insufficient data gathered, what the probable percentage of deaths would be for every year of life, in large communities living under similar conditions.
In illustration of what has been said, and as both interesting and instructive, the actual percentage of deaths comprised under the “Ungraduated Actuaries’ Experience Table No. 2” is herewith given in graphic representation:
The table shows the remarkable fact that, out of so large a number as 23,800 deaths, not a single individual died at ages eleven, sixteen, and ninety-four. This is due to the insufficient number of persons insured under twenty years, and the very small number living above
English Ungraduated Actuaries’ Experience Table No. 2.
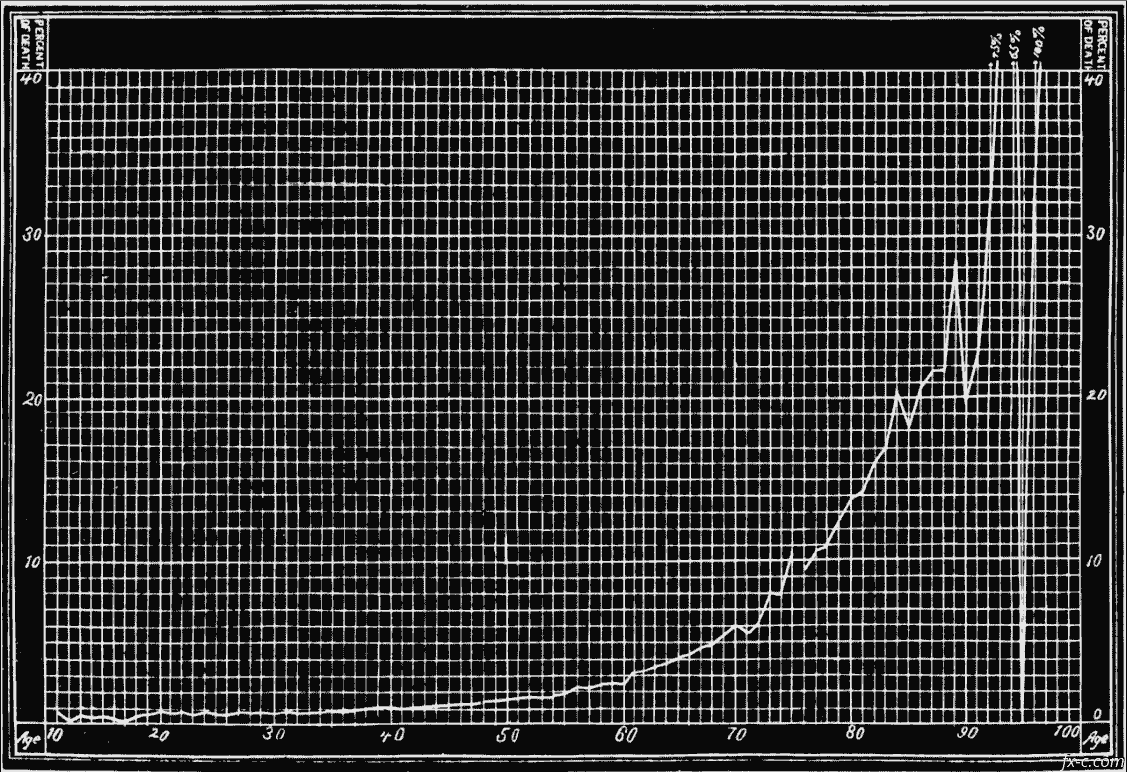
ninety years of age. The other most apparent fluctuations are a fall at age eighty-nine and a sudden rise at ages ninety-two and ninety-three. Here, again, for the same reasons, a very few deaths above or below the average cause large differences in the percentage. But more or less deviation was experienced for almost every year of life, although the small scale to which the representation is necessarily confined docs not clearly indicate it. The most superficial examination, however, must convince us that we are not dealing with accidents, but with a clearly pronounced tendency in the rate of mortality, disturbed only by minor causes.
Leaving for the time life-insurance experience, for the wider field of vital statistics generally, we have to note a most important step, in the introduction of the decennial census in England in 1801, and the adoption of a system of registering deaths, births, and marriages, begun in 1836.
The data were thus collected for constructing a mortality table, embracing the whole population of England. This task was undertaken by the Assistant Registrar-General, Dr. Farr, on the census of 1841, and is known as “English Life Table No. 1.” It is based on about 16,000,000 lives and 344,000 deaths. In 1863 he published a second, table called “English Life Table No. 2,” using the data of the census of 1841 and extending the deaths to three years previous to and three years subsequent to 1841. This period of seven years (1838 to 1844) furnished 2,436,648 deaths. Finally, in 1864, “English Life Table No. 3” was given to the public in the form of a distinct work. It was deduced from the two censuses of 1841 and 1851, and other records for the seventeen years from 1838 to 1854, embracing some 50,000,000 persons living and 6,470,000 deaths. Here, at length, we have a life-table on the largest scale, comprising the population of a whole country from birth upward. A graphic representation of the same is herewith presented, as that conveys a clearer picture to the mind than the reading of the numbers of the living and dying for every age.
On comparing Life Table No. 3 from ten years upward with the “Ungraduated Actuaries’ Experience Table No. 2,” it will be observed that the direction of the curve is very similar in both; but, while the one is absolutely smooth and even, the other is disturbed by the more or less violent deviations already referred to. The process of removing these unevennesses in the line, actuaries call graduating or adjusting. It is a very delicate and most important problem, for it involves no less than the effort to determine the law of mortality, freed from the accidental influences which experience has recorded. The outline of this law is, indeed, clearly defined, and can be traced in every table—a high rate of mortality in the first year of life, decreasing until the minimum is reached somewhere near the age of puberty, then rising very gradually, until with old age a very rapid increase takes place. But, while these general traits are well established, the details are subject to continual deviations.
We must assume that there is a fundamental law of life accompanying the organization of the human being, but that it is
English Life Table No. 3.
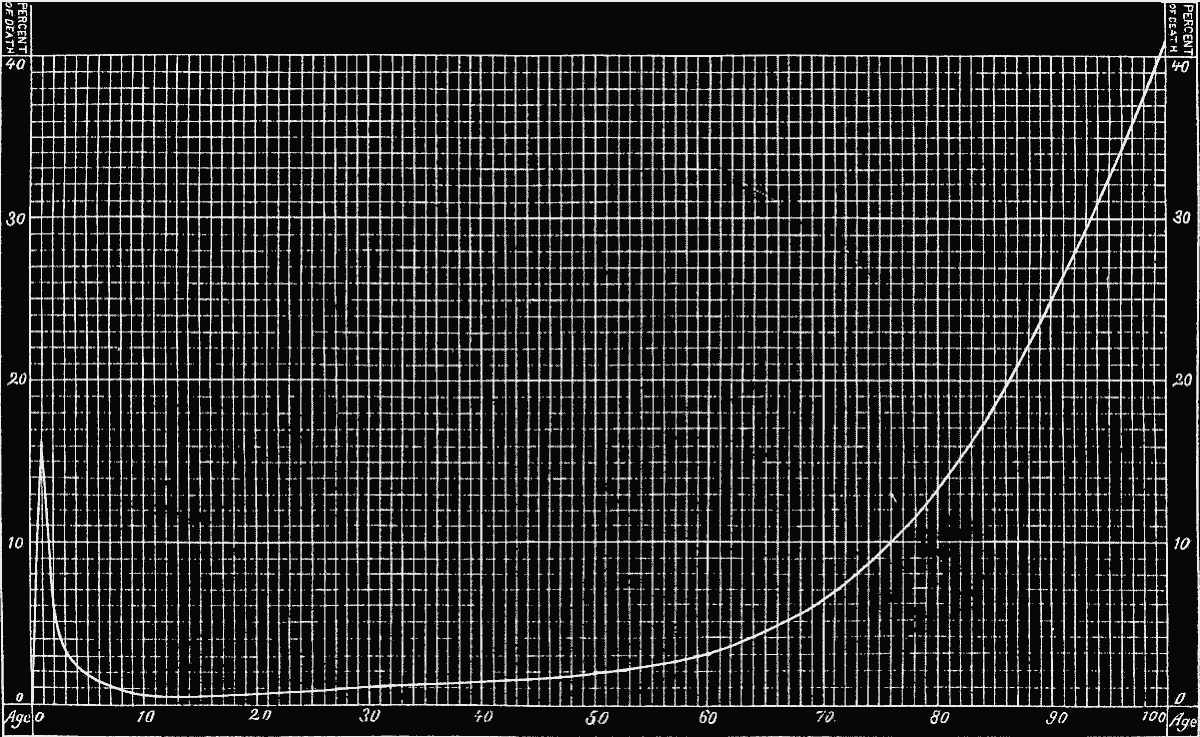
frequently traversed by many artificial and accidental influences. To determine the normal and eliminate the accidental conditions is the aim of theoretical inquiry. On the other hand, it may be urged that there is no normal standard of life nor of its surroundings, and that length of life is merely an expression of the sum total of social influences upon the organism. A community may be divided into ever so many groups, each of which will have its peculiarity, and the summary of all these units will give as resultant the average of life. Every graduated mortality table may, therefore, be considered only an approximate expression of the death-rate under the conditions and at the time of observation.
We may now follow “English Life Table No. 3” more in detail. It gives a separate record of both male and female life, and we may examine the mortality of males first.
The notation adopted refers to the percentage of death in the current year; meaning from birth to end of first year, 1 from beginning to end of second year of life, and so on:

Thus it appears that, with the exception of the period from fifteen to thirty-seven, where the larger mortality can be easily explained on physiological grounds, females have a far better chance of life than males. This is particularly marked in the first year of life, and after fifty-three years of age.
Some of the results deduced from this table will no doubt surprise many. It is not commonly assumed that age thirteen is the healthiest in life, or that so large a proportion of infants will reach as high an age as is here indicated. Nor is it generally known that more boys are born than girls, and that the weaker sex has such decided advantages in life over the stronger. But, while nearly five per cent, more male than female infants are born, the very reverse appears in the whole population, there being about five per cent, more females living than males. Of course, these proportions refer to England only, and they vary in different countries, according to conditions and influences that the reader can readily picture to himself.
English Life Table No. 3 marks an epoch in statistical science, and the results obtained are valuable and sufficiently reliable for practical purposes, but much yet remains to be done to satisfy scientific inquiry. An annual census, which is strongly urged, would allow a closer and more frequent examination of facts, and reduce mathematical speculation to a minimum.
One question of grave importance can not yet be considered as definitively settled; it is whether the rate of mortality is steadily declining, and the duration of life is correspondingly extending. In a general way, and as compared with former centuries, there can be no doubt that a marked improvement is to be found. Take the population of England as an illustration:
| It was | estimated in | 1651 at | 5,450,000 |
|---|---|---|---|
| " | " | 1751 at | 6,400,000 |
| Census of | 1801 at | 8,892,536 | |
| " | 1851 at | 17,927,609 |

This shows an increase of seventeen and a half per cent, for the century from 1651 to 1751, of thirty-nine per cent, for the fifty years to 1801, and of one hundred and one and a half per cent, for fifty years to 1851.
These rapid strides are not astonishing when we consider the epidemics, the internal strife, the famines, and insufficient means of communication, the disorderly and unsettled habits of former times, and compare them with the better hygiene, the greater comforts, and the generally refining influences of the present. But this increasing ratio of growth may be due either to a larger percentage of births, or to a smaller proportion of deaths, or to both causes combined. Statistics seem to indicate that both factors are even now contributing to this result. In 1841, out of 1,000 of the population, 15·4 were married during the year, and in 1876 the number had gradually risen to 17 per 1,000. So that, in spite of large cities and the greater difficulty of supporting families, the growing tendency to settled and more regular habits is exhibited in the larger number of marriages. The result is an increasing number of births in proportion to the population. In 1841, 512,158 children were born, being 32·2 per 1,000, while in 1870 the number was 887,464, or 36·6 per 1,000, which is an increase of about twenty-five per cent. The deaths, on the other hand, remained nearly stationary, being 21·6 per 1,000 in 1841 to 21·9 in 1876. The ratio of deaths to births, therefore, stood as 1 to 1·49 in 1841, while in 1876 it was as 1 to 1·74.
The preponderance of young families, however, ought to make the death-rate very much higher, as the mortality at the young ages is very large. Since it remained nearly unchanged, while the marriages and births increased, it would indicate that the average duration of life was being extended. For special localities like large cities, it is well known that sanitary measures and other causes are producing constant improvement; but there are many counteracting conditions to be considered. With an improved system of registration and more frequent enumerations of the people, data will be obtained for computing and comparing life tables at shorter intervals, and there can be no doubt that, in spite of increasing difficulties, the beneficial influences of higher civilization will be found to tend to a steady prolongation of human life.
Recurring after this digression to the experience of life-insurance companies, we will compare English Life Table No. 3 from twenty years upward with the two tables most in use, the Actuaries’ Experience Table No. 1 and the American Experience Table. The percentages are given, in preference to the number of living and dying for each period:
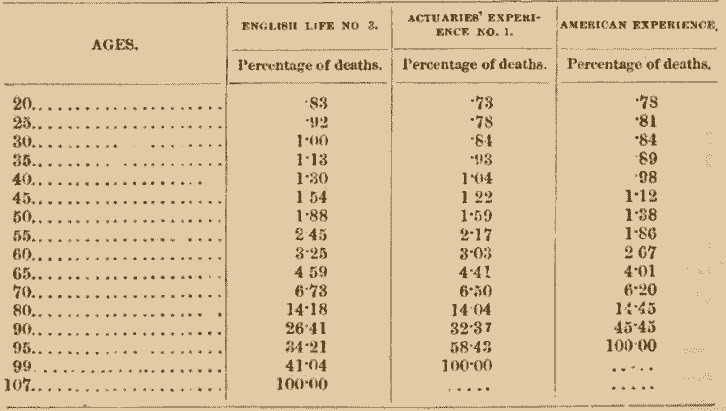
While the two experience tables are very similar, and represent about the same social conditions, the well-to-do middle classes, in this country and in England, the American table has a peculiarity characteristic of life in the United States. At the younger ages, up to thirty years, the mortality is greater, while from thirty to seventy years it is somewhat less than in England. During this latter, the most active period of life, the strain upon the system is very great in this country, and the vital forces are used up to such an extent that after seventy years the death-rate rises rapidly. The table ends at ninety-five, while the English is carried to ninety-nine. It may also be mentioned here that female life has proved less favorable than male life to insurance companies, while it will be remembered that the very reverse has been observed in the community at large. The next point that will attract attention is, that the English life table, representing the average life of the whole population, does not range so much above the insurance tables as might be supposed. Insurance companies select only healthy individuals by medical examination, and almost exclusively from the better classes and occupations. Why, then, is the difference not greater? Some of the reasons can be readily given. First, there is a constant effort on the part of the public to foist impaired lives upon the insurers. No amount of care or precaution can detect all misrepresentation or trace every inducement to fraud and self-destruction, and, while it may amount to less than some assume, it undoubtedly reduces the standard of absolute health. Of far greater importance is the observation that the effect of selection nearly wears away in about five years. Taking a class of live? selected by medical examination, say at twenty-five years, it will show a reduced mortality during the first year; but after five years, at age thirty, very nearly the usual average is again reached. For, while the diseased are excluded from the selected class, a certain number of these sound lives will find their health to fail from year to year. Were those admitted at twenty-five years to be reexamined at age thirty, so many sick and ailing would be among them that the advantages of selection would be found to have largely disappeared.
Registrar-General Farr estimates 27 out of 1,000 of the whole population, between the ages of twenty and sixty, to suffer from some kind of disease or other, be it hereditary, chronic, recurrent, or acute. Consumption, he thinks, though varied in duration, seems to average about two years. The higher the age, the greater the value of selection; and, the older the members of a life-insurance company become, the more do they approximate the health of the community at large.
Another factor that operates as a selection against the mortality experience is what is called lapses. A large number of policies are constantly allowed to terminate through the indifference of the insured, and for various other reasons. But, while the healthy often forfeit their insurance upon slight provocation, there are few indeed, of those that think their health impaired, that will do so. The result is, that an undue proportion of the sickly will remain, and exert a deteriorating influence upon the average mortality.
Finally, it must not be forgotten that there is, after all, a considerable difference in the middle ages between the English life table and the insurance tables, particularly the American Experience Table. This latter, Mr. Romans states, has the effect of selection carefully eliminated, and therefore indicates a higher rate of mortality than the actual experience. As a matter of fact, all well-managed insurance companies, doing a sufficiently large business to furnish the basis for reliable averages, and having a constant accession of new lives experience more or less gain over the tables in use.
Before dismissing this subject, one question of a general character yet remains to be answered, viz., how do, or may, epidemics affect the average rate of mortality?
As regards the possibilities of the future, it is strictly a problem for medical and sanitary science; but we may be allowed to draw some inferences from the past records of a well-ordered state.
In 1849 a cholera epidemic, of a very malignant type, prevailed in England, considerably increasing the mortality for that year.
The number of deaths for the five years from 1848 to 1852 were as follows:
| 1848 | 398,385 |
|---|---|
| 1849 | 440,883 |
| 1850 | 368,602 |
| 1851 | 395,396 |
| 1852 | 407,135 |
| ————— | |
| 2,010,401 |
It will be noticed that in 1849 the increase over the previous year was about 42,000, while in the following year, 1850, there was a falling off to 30,000 below the number of deaths in 1848. For the period of five years from 1848 to 1852 the annual average of 400,000 remained undisturbed. This would indicate that, when through a powerful influence an excessive death-rate prevails, a large proportion of the weak and sickly is carried off, so that by way of compensation the surviving, healthier population will for a time show a mortality below the average. It is also well known that such inflictions are largely confined to the dirtiest and most crowded quarters, and carry off principally the poor and improvident. As these classes do not insure their lives, the mortality experience of insurance companies is no more likely to be seriously affected by epidemics in the future than it has been in the past.
THE PRACTICAL BUSINESS OF LIFE INSURANCE. #
THE mortality tables, forming the theoretical basis of life insurance, having been explained, it remains to be shown how they are employed in practice. There is a fundamental difference between life and fire or marine insurance that must first be considered. The hazard attaching to a building or a ship may remain unchanged for a very long term of years, and the rate of premium once determined need not be altered. Such property is usually insured for one year at a time, and renewed as often as desirable. But the same methods can not be applied to human life. If the policy were to terminate annually, and a new examination could be demanded, many persons whose health had become impaired would be declined at the beginning of every new year. Then, as has been shown, from a very young age, upward, the rate of mortality constantly increases. That would necessitate a higher premium charge from year to year, so that, finally, a person who should be fortunate enough to reach the highest age of the table would have to pay one hundred per cent, for that one year. It requires no argument to prove such a system impracticable, and therefore the plan of fixing one uniform periodic premium for the whole term of the proposed insurance has been adopted.
The following table shows, in one column, the amount of net premium that must be paid at the beginning of every year to insure 81,000 for that year; and, in the other column, the equal net annual premium to insure for life.
By net premium is meant the amount calculated from a certain mortality table, and rate of interest, without any addition for expenses.
In all illustrations hereafter given the American Experience Table and four and a half per cent, interest will be employed, that being the official standard for the State of New York.
| Age. | Net premium | Net annual | Age. | Net premium | Net annual |
|---|---|---|---|---|---|
| for one year. | premium for life. | for one year. | premium for life. | ||
| 20 | $7 47 | $11 97 | 60 | $25 54 | $54 14 |
| 21 | 7 51 | 12 23 | 70 | 59 61 | 97 00 |
| 22 | 7 57 | 12 50 | 80 | 138 24 | 188 20 |
| 90 | 434 96 | 494 33 | |||
| 30 | 8 06 | 15 34 | 94 | 820 22 | 836 69 |
| 40 | 9 37 | 21 30 | 95 | 956 93 | 956 93 |
| 50 | 13 19 | 32 49 |
From this table it appears that, to insure $1,000 for one year at a time, it would cost $7.47 at age 20, and that the amount would have to be continually increased, until at age 90 it would be $434.96, while the same purpose would be accomplished for an equal annual premium of $11.97. The somewhat larger expense in the earlier years of insurance avoids the necessity of enormous charges at the high ages.
The method of arriving at the equal annual premium is based upon very plain reasoning, and can be explained in a simple manner.
Let us assume, with the American Experience Table, that, out of 100,000 persons at age 10, there remain 847 living at age 90, and that they die, according to the table, as follows:
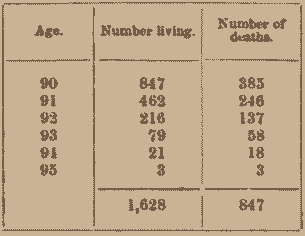
Were these 847 to form an association, based on the condition that the payments remain equal throughout, and be collected from the survivors at the beginning of each year, and that $1 be paid at the death of each member, there would be 1,628 contributions during the whole period, to provide for 847 death-claims. The requisite annual premium would therefore be 8471628 dollar, be \(\frac{847}{1628}\) dollar, or $0.52027 (52 + cents). Let us examine the working of this fund:

One important element, however, the investment of money at interest, has been omitted in the above illustration, and will be introduced now. It has already been stated that premiums are payable at the beginning, while death-claims are due at the end, of the same year. To bring these different amounts and dates to a common basis we must determine the present value of each, at the age at which the insurance begins. Knowing, from the table, the amounts of the contributions and the number of deaths and the time at which they become due, it is to be ascertained what amount of money deposited at the beginning of the period, improved at compound interest, would be equivalent to the total of these sums.
The present value of $1 at the beginning of the year, at 4\(\frac{1}{2}\) per cent. interest, is $0·9569; that is to say, $0·9569 invested at 4\(\frac{1}{2}\) per cent. interest will amount to $1 at the end of the year. The present value of $l for two years is $0·9157, for three years $0·8763; or these amounts, improved at 4\(\frac{1}{2}\) per cent, compound interest, will become $1 by the end of these years.
Applying this principle to the class of 847 persons under consideration, and assuming each contribution and each death-claim to be $1, we need only multiply these by the present value corresponding to each year, bearing in mind that the living pay in advance, while the death-claims are due at the end of the year:
| Age. | Living. | Deaths. | |||
|---|---|---|---|---|---|
| 90 | 847 X $1= | $847 00 | 385 X ·9569 = | $368 41 | |
| 91 | 462 X ·9569 = | 442 10 | 246 X ·9157 = | 225 26 | |
| 92 | 216 X ·9157 = | 197 79 | 137 X ·8763 = | 120 05 | |
| 93 | 79 X ·8763 = | 69 23 | 58 X ·8386 = | 48 64 | |
| 94 | 21 X ·8386 = | 17 61 | 18 X ·8025 = | 14 44 | |
| 95 | 3 X ·8025 = | 2 41 | 3 X ·7679 = | 2 30 | |
| $1,576 14 | $779 10 |
The above calculation shows the present value of the 1,628 contributions, at $1 each, to be $1,570.14, and the present value of the 847 death-claims to be $779.10; therefore, to meet these latter, the contributions need only be, instead of one dollar, \(\frac{77910}{157614}\) of one dollar, or $0·49432 (49 \(+\) cents). The item of interest has reduced the premium to $0·49432, when, without it, it would have been $0·52027.
Similarly to the annual premium, any other mode of payment may be determined; say, for instance, one single premium for life. At age 90 the present value of all future death-claims is $779.10, and there are 847 persons to provide for the same; therefore, each one must contribute \(\frac{779.10}{847}\), or $0·91987 in advance, that being the one single premium for life.
The limits of a magazine article do not permit more extended illustrations, but the reader can readily reason out for himself how premiums, insuring for life in a limited number of payments, and various other adaptations in vogue, all based upon the same principles, may be arrived at.
Let us now apply the annual premium of $0·49432, as above ascertained, to the insurance fund, and follow its working to the end, computing interest at 4\(\frac{1}{2}\) per cent.:

It will be observed that, at the end of every year, with the exception of the last one, an unexpended balance remains; dividing this by the number of survivors, we get the amount that applies to each individual living at that period. This is called the net valuation, or, more commonly, the reserve for each policy.
At the ages we have under consideration, the reserve would be as follows:
 While the reserve, as here given, is strictly correct in amount as well as in principle, other methods of calculation are employed in practice; but, for a simple explanation, the plan here adopted will probably serve better than any other. The difficulty has also been that the very high age of ninety had to be selected for the above illustrations, because every computation has to be carried to the end of the table, which would be very lengthy and tedious for a young age. But, the explanation having been given, a closer inspection of the reserves applying to age twenty will afford a broader insight into the subject:
While the reserve, as here given, is strictly correct in amount as well as in principle, other methods of calculation are employed in practice; but, for a simple explanation, the plan here adopted will probably serve better than any other. The difficulty has also been that the very high age of ninety had to be selected for the above illustrations, because every computation has to be carried to the end of the table, which would be very lengthy and tedious for a young age. But, the explanation having been given, a closer inspection of the reserves applying to age twenty will afford a broader insight into the subject:
Age 20—Net Annual Premium $11.97 per $1,000.
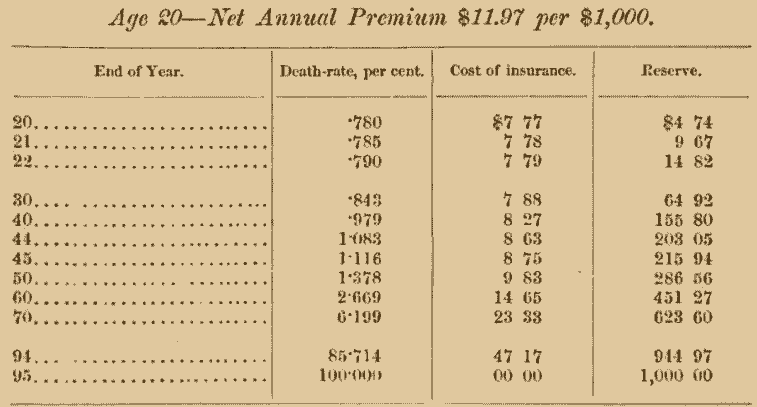
From the above table it will be seen that the annual premium may be looked upon as consisting of two parts, one defraying the annual cost of insurance dependent upon the death-rate, the other put aside as a reserve fund. Up to a certain period the premium is larger than the actual cost of insurance, but a time arrives when it does not suffice, and then a part of the interest on the reserve must contribute the difference. It will be noticed that the reserve grows constantly, so that by the end of the year 94 it is $944.97, and, with the annual premium of $11.97, due at the beginning of year 95, amounts to $956.94, which, invested at 4\(\frac{1}{2}\) per cent, interest, will by the end of the year produce the sum of $1,000. Theoretically, then, there is no loss from a person dying according to the last year of the mortality table, because the whole amount of the sum insured has already accumulated under the reserve.
This reserve, too, may in a certain sense be said to have a twofold function: it not only provides for the future, but also annually reduces the amount at risk, whereby the cost of insurance becomes less than it would otherwise be. Thus, by the above table for the year 45, the cost of insurance is only $8.75, while the death-rate would amount to $11.16 per $1,000. The fact that the reserve has reached $215.94, and the amount at risk is only $784.06, reduces the cost from $11.16 to $8.75. For the year 94 the death-rate would amount to $857.14 per $1,000, while the cost of insurance is only $47.17, since the reserve has accumulated to $944.97, leaving but $55.03 at risk.
As a final illustration of the whole method take the reserve at the end of year 44, $203.05, add the annual premium of $11.97, being together $215.02, invest at 4\(\frac{1}{2}\) per cent, interest, and it will amount to $224.69; deduct the cost of insurance, $8.75 (being the amount at risk $784.06 X 1·116 per cent., the death-rate), and the balance remaining, 8215.94, is the reserve at the end of year 45.
But, however instructive these details, it may be well, to avoid confusion, to sum up the whole process in the statement that the annual premium is a device to collect a larger amount than the death-rate in the earlier years of insurance, and to use these over-payments, improved at compound interest, to meet the deficiencies which arise in later years. The premium and reserve are so nicely adjusted that they are strictly equitable for the living as well as the dying at every year of life.
The view of the reserve or net valuation here presented is distinctively American. It has been embodied in State legislation, and has an important bearing upon the question of surrender values, presently to be considered. There are other methods for determine: the valuation, which take into account all future payments due, and all losses and expenses to be incurred to the end of the table; but these are questions beyond the scope of this article.
To the net premium of which we have treated, a certain percentage is added to defray expenses and to provide for contingencies; it is called loading, and together with the net premium constitutes what is known as gross or office premium. In mutual companies, the only ones that will be here considered, the loading is made higher than any probable exigency will demand, so as to be absolutely safe. At fixed periods the amount collected, in excess of actual cost, is distributed among the contributing members. It is erroneously called “profits” or “dividends,” when, in reality, it is only a return of unexpended assessments. When the system was new and untried, it was not thought prudent to make such restitution oftener than every five years. Gradually experience led to greater confidence, and competition introduced the practice of annual “dividends.” These are principally derived from the higher rate of interest realized than the legal standard assumes, from a lower mortality than the table estimates, and from the excess of loading over actual expenses. Various ways of distributing this surplus have been in use, but the so-called “contribution plan,” now universally adopted in the United States, is unquestionably the most equitable ever devised, as it returns to every member precisely his proportion of the over-payments. It may be best explained by an illustration.
Take a policy issued at 25, at an annual premium of $19.89, on which a cash dividend of $6.72 has been declared at the end of year 38. Assume the expenses applying to this policy to be equal to about 10 per cent, of the annual premium, the average rate of interest realized 5\(\frac{1}{2}\) per cent., and the actual mortality experience to be 10 per cent, less than the table indicates, the account would then stand as follows:
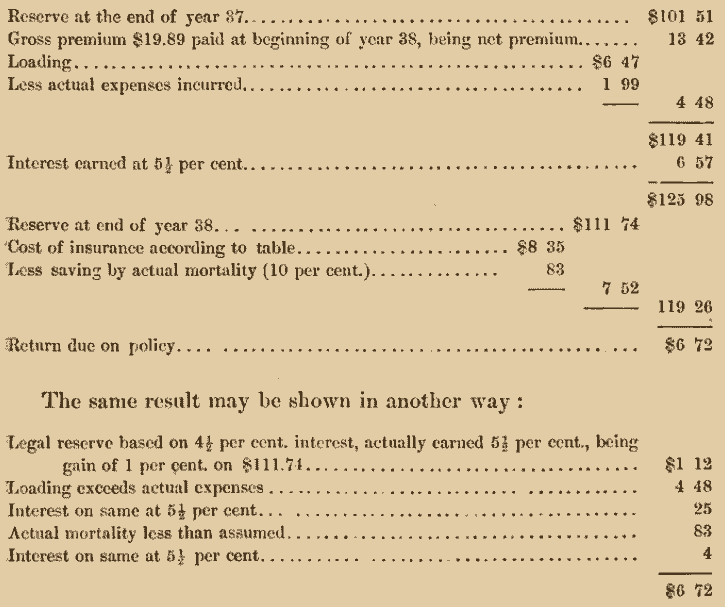
Of course, there may be other items of gain or loss besides those enumerated in the above illustration.
Most companies give policy-holders the option of either taking a cash return, or having the amount converted into a “reversionary dividend,” payable with the policy; that is, simply to purchase insurance for a single premium. The above cash dividend of $6.72 would give a net reversionary dividend of $20.82 (the net single premium for $1.00 at age 39 being $0·32283); but of course some deduction must be made for expenses of management.
These reversionary additions form a very large item with old institutions, one leading company alone having over $25,000,000 in force.
Intimately connected with the reserves and dividends, and next in importance, is the question how lapsed or forfeited policies should be treated. Probably no theoretical point has been so hotly contested, and certainly none has offered equal difficulties in practice. In the early days of the institution, when it was prudent to err on the side of safety, the view prevailed that a policy was a contract for life, from which neither party could withdraw. Instead of a single premium in advance, annual account payments were accepted, but it was thought that a violation of this condition could only be regulated by absolute forfeiture of all previous contributions. As the business grew in importance, and long experience proved it grounded on reliable foundations, the harshness of this rule began to attract attention.
In England Dr. Farr advised the issuing of non-forfeitable policies, and the allowance of a definite cash surrender value on them. In this country the Insurance Commissioner of Massachusetts first brought the subject before the Legislature of that State, and a non-forfeiture law was passed in 1861. In opposition to the views held by actuaries of the old school, a tendency extreme in the other direction now began to assert itself. It was contended that the reserve pertaining to each policy should be considered equivalent to a deposit in a savings-bank, to be withdrawn at the pleasure of each individual insurer. This position was combated as wrong in theory, and as absolutely subversive of the business in practice. Insurance when applied to the individual becomes an absurdity, and it can only be safely conducted on averages dependent upon large aggregates. A person that insures for life virtually agrees to contribute to the death-claims of other members as long as he himself lives, and should he withdraw ought to pay his share of the liabilities assumed and the expenses of management attendant thereon. It becomes the duty of an insurance company to prevent the unnecessary withdrawal of its members, and self-preservation compels it to constantly strive to acquire new lives to retain the institution in a prosperous condition. Therefore, while it would be unjust to confiscate the whole accumulated reserve on lapsed policies. it is but fair that such charge be made as to fully compensate the association for the loss of a withdrawing member.
These views may be considered as the equitable, middle course between two extreme positions, and they are now very generally conceded and adopted in practice. Policies are made non-forfeitable after two or three annual payments, and when lapsed, if presented within reasonable time, either paid-up insurance is granted or a percentage of the reserve allowed as cash surrender value. A few, indeed, have gone further, and printed in the contract the fixed cash surrender value that may be obtained at the end of every year. This innovation is not unlikely to be permanently ingrafted upon the business, and even now there is hardly a reputable company that declines to purchase its own policies when presented at the proper time; and the amounts thus expended are far greater than is generally known. One leading company of this State, whose annual premium income for 1879 was about $12,500,000, paid over $4,500,000 for surrendered policies. Various intricate formulas have been devised by actuaries to determine the strictly equitable surrender value, which, however, as far as the general reader is concerned, all culminate in a larger or smaller percentage of the reserve.
While proper agitation, competition, and a sense of justice, brought about a fair adjustment of cash surrender values, the question of paid up insurance has been definitively determined in New York by the enactment of a statute, which went into effect January 1, 1880. It provides that when a policy shall lapse for the non-payment of premium, after being in force three years, the reserve and dividend additions on such policy shall, on demand made within six months after such lapse (unless the provisions of the statute had been specifically waived), be taken as a single premium at the published rates of the company, and be applied either to continue the policy in force at its full amount, so long as such single premium will purchase temporary insurance for that amount, or to purchase paid-up insurance, payable at the same time as the original insurance; provided, however, that the net value of the insurance given for such single premium shall in no case be less than two thirds of the entire reserve. That is to say, that the whole amount of the policy shall remain in force for such a length of time as no less than two thirds of the net reserve will purchase, or that the amount of the policy shall be reduced correspondingly, and be made to expire at the time originally fixed by the policy. In principle, therefore, the question may be considered as permanently settled, and new methods will certainly be devised to adjust minor practical difficulties upon an equitable basis.
Still, many crude ideas yet prevail among the insuring public, which lead to misunderstandings that ought not to exist. Some intelligent men, even, imagine that a company should be compelled to reinstate a lapsed policy without reëxamination of the insured life, or that, at least, the whole amount of premiums paid ought to be returned, since no loss has occurred. However absurd such notions, they have caused much dissatisfaction, and, as they spring from a total misconception of the aims and functions of the institution, they ought to be dispelled. The companies themselves are not free from blame, however, for permitting many false impressions to gain ground. Nothing can be more mischievous than the assertion that life insurance is a profitable investment for money in the ordinary acceptation of that phrase. It is a provision against a contingency to which every human being is subject. A proper appreciation of its great benefits would prompt most men to seek its protection as far as their means permitted. To the majority of insurers, however, it is an actual expense, though allotted among them upon the most equitable basis. On the other hand, the amount of premiums paid can never be totally lost, since every life policy must eventually become a death-claim. But only those should insure who really require it and can continue payments to the end. Had this always been understood, many policy-holders would have been spared disappointment and suffering when sober reaction followed a period of wild inflation.
One of the evils resulting from dissatisfaction with insurance companies has been the formation, all over the country, of so-called cooperative (latterly mutual benefit) life associations. They are based on what has already been shown as utterly impracticable—the collection of contributions on the death of members, with no fixed premiums or adequate accumulation of reserves. When the lives are newly selected, and not much above middle age, there is, at first, an appearance of saving over regular premiums. But, as they get older and the rate of mortality rises rapidly, the contributions become onerous, and, there being nothing to forfeit, the healthy lives withdraw, leaving a constantly increasing preponderance of impaired lives. The association breaks up, and those most in need of insurance can no longer obtain it from regular companies. The fallacy consists in assuming a continuous increase of new young lives that are willing to bear the burdens of the old members; an infatuation that never lasts long. It seems almost incredible that, in the face of well-established scientific principles and a century’s experience, such crude experiments should again be introduced, as though they were a new invention. They deserve no better name than frauds, originated either by designing men to plunder the credulous or by those so grossly ignorant as to be no less culpable. Well have they merited the name current in insurance parlance, “the co-duperatives.”
We have now touched upon most of the distinctive features of life insurance that interest the general reader, and but little remains to be said of the general management. It has been shown that next in importance to the collection of premiums is the accumulation of a reserve, which must earn at least the minimum rate of interest assumed as the basis of calculation. This is no easy task in the present condition of the money market, and exceptional skill, prudence, and forethought, are required to secure safe and profitable investments. It must be remembered, too, that theoretically all the funds on hand are supposed to bring interest, while in practice a considerable part must always remain unemployed, so that the average rate realized is less than the current rate of interest. On the other hand, well-managed companies accumulate a surplus over the net reserve, and have their interest income largely increased from this source. Still more important is the fact, as far as New York is concerned, that, since Massachusetts and some other States have established four per cent, as the legal standard for reserve, and all companies desire to transact business in those States, they keep their surplus sufficiently high to be virtually on a four per cent, basis. Whether a lower rate than this will be realized on safe investments in the next quarter of a century, expert financiers and economists seem hardly prepared to answer; but, should a reduction to a three and a half per cent, standard become necessary, it would only temporarily incommode our sound offices.
With mortality tables as reliable as any human estimate can make them, and with reserves based on a sufficiently low rate of interest, the management of a life-insurance company does not materially differ from that of other moneyed institutions. The proper selection of business and the safe investment of funds require prudence and sagacity, and devolve great responsibility upon executive officers. But mutual-insurance companies (and nearly all stock companies in the United States also embody the mutual principle) have a margin far above any probable exigency, in the excessive loading of premiums. This very safeguard, it is true, may be perverted, and in some cases has been a temptation to abuse and extravagance. A life-insurance company once fairly established, however, ought to be as safe as any other financial institution, and, where failure occurs, it may always be traced to either gross mismanagement or intentional fraud. State supervision, which has been of great benefit to the system and to the community, can never supplant individual judgment or probity. In fact, it ought to be limited to prescribing minimum reserves, the character of investments, and the publication of truthful statements of the condition of companies.
While life insurance is of comparatively recent date in the United States (the oldest company now in business having been organized in 1843), its development has been so rapid as to have probably surpassed that of every other country. The following table shows the condition of the business, as reported to the New York department, in its infancy in 1859, its period of highest inflation in 1870, and at the lowest point of reaction in 1879:
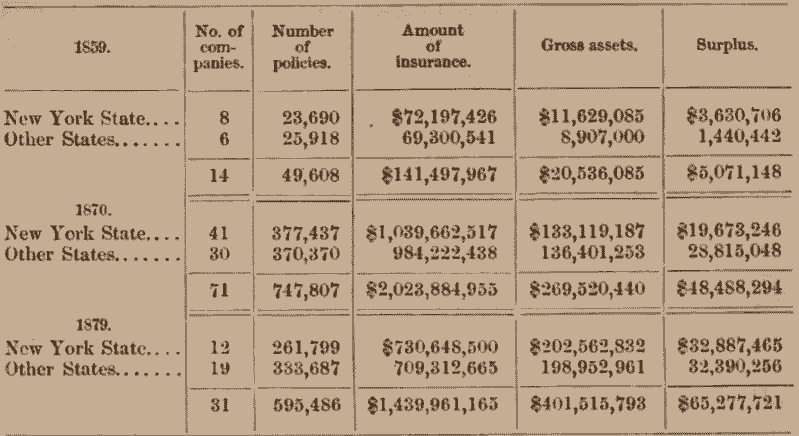
The number of companies rose from fourteen to seventy-one in eleven years, and fell to thirty-one in the following nine years, while the amount insured was only reduced by about 25 per cent. Compared with other institutions, this shrinkage during a period of general retrenchment is not large. With about 600,000 policies in force, $400,000,000 of assets and $65,000,000 of net surplus, the success of life insurance is really astonishing. As a cooperative enterprise, in the truest sense of the word, it outranks every other in the means employed. Scientific principles are applied to the solution of an intricate social problem, and result in the most equitable division of burdens. The aims and purposes are most exalted, too. Other associations combine individuals to cooperate with a view to their own present support and immediate enjoyment, while this institution is based upon abstention, self-imposed for other future beneficiaries.
With its usefulness not yet fully appreciated, its wide field of application not thoroughly understood, we may well be thankful for what it has already accomplished, and be proud of it as an exponent of the civilization and of the times in which we live.
These tontine associations must not be confounded with the so-called tontine life-insurance policies issued by some companies at the present day. These latter have simply borrowed the name, while in other respects they are like ordinary life-insurance policies; only that, instead of having dividends declared annually, they are held back for fixed periods, say ten or fifteen years, and then distributed among the surviving members. ↩︎